

[Note: For the quick summary of normalized fractional blockage, with tables, see this link.]
The S-Pol radar was sited a few meters above sea level on an island in the Addu Atoll chain, Maldives, Indian Ocean. The radar did not have a fully clear horizon, with trees located on the atoll from about 180 degrees azimuth, through the west, and almost to due north. Due east of the radar, a shipping wharf created some blockage through a few degrees of azimuth. At an azimuth of 290 degrees, a tall tower had some impact on radar signal transmission; several shorter towers are found to the NNW.
A full panoramic image (taken from the catwalk below the S-Pol antenna) is available for review.
The DYNAMO S-Pol siting represents about the simplist conceptual conditions for beam blockage: all potential blockage is relatively near the radar, the blockage is essentially a single line of obstructions (the narrow width of the atoll causes this), and all obstructions are optically visible on a relatively clear day. There are essentially no obstructions beyond/behind those visible in the panoramic image.
Azimuthally-dependent estimates of blockage may be made from radar estimated precipitation. Under the best of circumstances, and provided with a long enough integration time, it might be expected that precipitation should be approximately uniform in all directions around a radar. Additionally, the difference in calculated integrated precipitation at one elevation angle should vary only slightly from that calculated for the next nearest elevation angle (assuming no blockage and an absence of features like a bright band). Both of these assumptions are easily tested for S-Pol in DYNAMO.
Since S-Pol is a dual polarimetric radar, there are a number of precip estimators that can be computed (see Rain Rate Computation). Additionally, some of these estimators should be resistant to partial beam blockage, providing better estimates than a direct reflectivity estimate, when the beam is partially blocked. Analysis of the ratio of azimuth-dependent precip for the different rates should provide insight as to which rates are better estimators under conditions of partial blockage.
During the DYNAMO period, S-Pol observed significant precipitation on 30 different UTC days. For each of these 30 days, every surveillance volume was analysed, and total precipitation along each azimuth was computed and summed for that day (totals for the days were later combined). The precip summation for S-Pol was further limited to ranges of 17 through 70 km, to avoid near-in clutter caused by the atoll and to avoid excessive beam broadening, as well as to limit the potential for one of the low-elevation beams to hit a freezing layer (generally above the 4km height). Only the lowest four tilts, at 0.5, 1.5, 2.5, and 3.5 degrees elevation were analyzed. Analysis was further restricted to only those gates of data that had valid measurements of the KDP-based rain rate (RATE_KDP). This last condition is rather restrictive, since RATE_KDP requires a fairly long multiple-gate run of filtered differential phase data. Because all other precip rates have values when RATE_KDP exists, this restriction ensures that all of our different precip rate comparisions have data sets with the same number of points.
Note that filtering on "RATE_KDP exists", does restrict our available data set. Total number of gates over the 30-days of analysis is approximately 10,300,000. This is a substantial number, but apparently not enough data points to ensure azimuthal uniformity of along-beam integrated precipitation. The following figure shows the azimuthal variation of precip for two rain rates, RATE_KDP(@2.5) and RATE_ZH(@2.5):
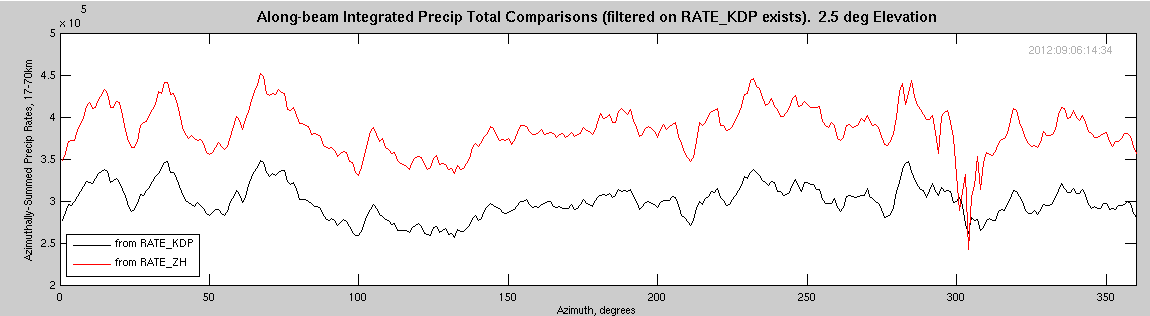
Note the following:
The uniformity of precipitation with varying elevation angle is shown in the next figure. Here, all plots are for RATE_KDP, where the rate at a given elevation angle is compared to the rate at 3.5 degrees elevation.
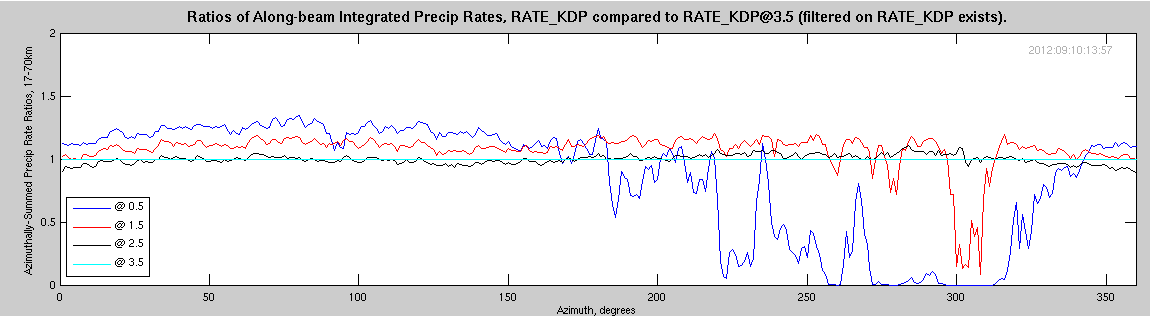
Notes:
A different perspective is gained by comparing two different rates to each other at the same elevation angle. In the next figure, RATE_ZH is compared to RATE_KDP, both at the same elevation angle. Over the open ocean, the comparison lines are very flat, except where the wharf exists (the largest variability is in the lowest tilt). Looking toward the trees, it is obvious that the lowest elevation angle is not usable, while the rates shown by the KDP estimator at 1.5 and 2.5 degrees seems more robust than the RATE_ZH (however, there is still some blockage of the RATE_KDP estimator).
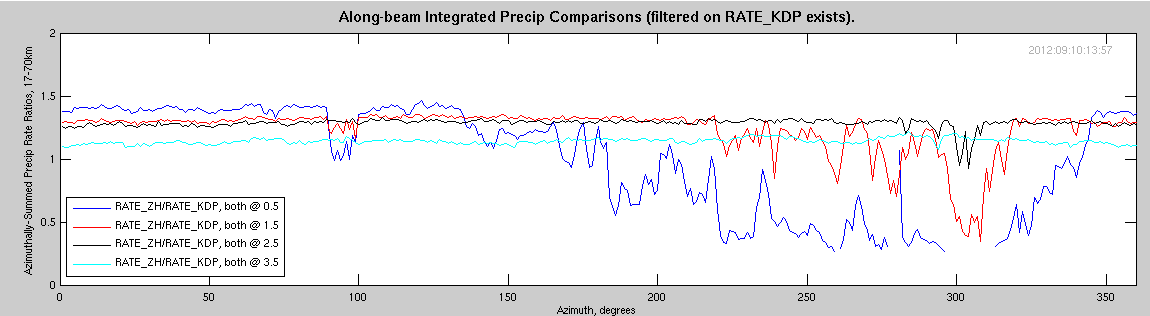
Finally, two plots are shown comparing the RATE_ZH (at various angles) to the RATE_KDP at either 2.5 degrees, or 3.5 degrees.
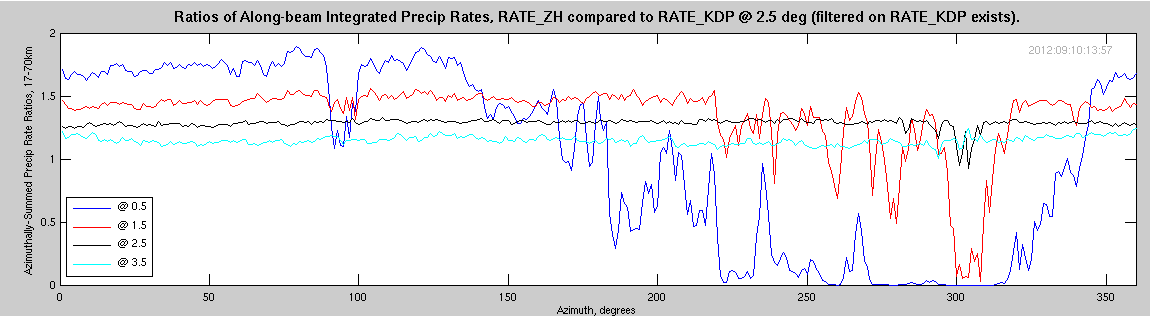
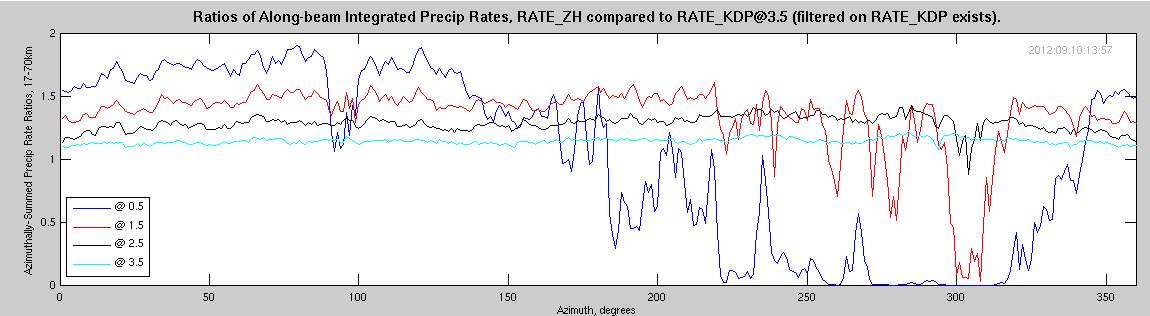
From these and the previous plots, we may assert:
A compressed panoramic image is provided, below. In this image, the vertical scale has been expanded by a factor of 4. A heavily JavaScript-abused page is available that allows overlay of this image over most of the plots shown (above), providing a really good perspective on blockage caused by the various elements visible along the S-Pol sight horizion.

Radar noise power is affected by the microwave glow of thermal emitters in the path of the radar beam. It is expected that the noise power can be used to estimate beam blockage for power-dependent radar variables (i.e., for dBZ, dBm, etc., but not for KDP). We are currently in the process of performing this noise power analysis, with results to be reported during the 2013 AMS Annual Meeting.
A very preliminary plot of results is available for a single elevation. This plot uses the full precip data set for RATE_ZH, compared to a single sweep of noise power data.
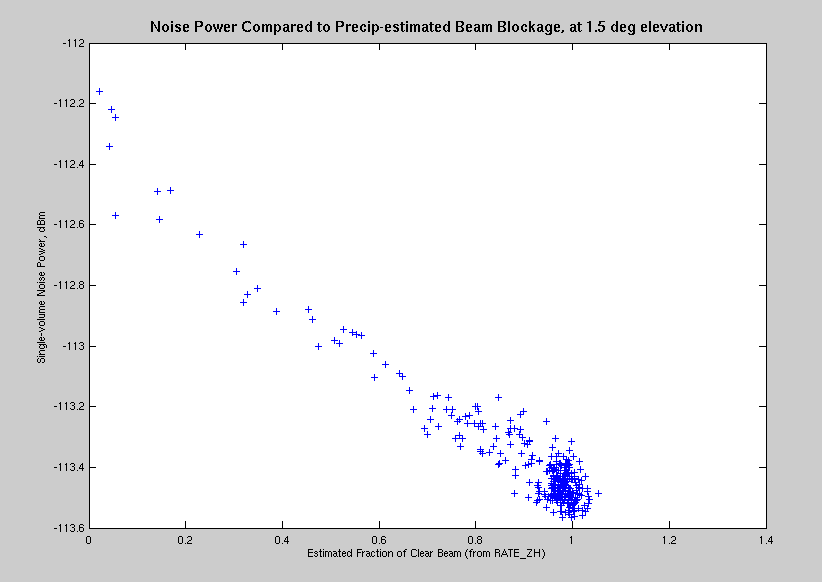
[Aside: why should this look like a linear relationship?]
Please see the reference on Noise Power Estimates of ... for details on an estimate of beam blockage through optical techniques.
[all additional items have been completed]
This work will be continued, as time permits.
Two main routines were required to compute azimuth-dependent integrated precipitation totals. These routines were used with data access subroutines detailed elsewhere. The first routine is run on each UTC day of significant precipitation, and the second routine compiles the results from the multiple daily runs of the first routine.