

Instantaneous rain rate estimators were computed by five different methods in real time. A rain rate estimate was determined for every gate (every beam, every tilt). Gate-by-gate time integration of a rain rate for the lowest tilt will provide an estimate of total accumulated rainfall over the region covered by the S-Pol radar. Rain rates in non-liquid precipitation areas should be ignored as they will be in error (i.e., ignore any values about the freezing level).
Clutter-filtered S-band horizontal reflectivity was used in computations. When Zdr is used, this is the clutter-filtered, bias-removed Zdr. KDP is also the clutter-removed S-band value.
Both ZH and ZDR are preprocessed through application of an along-beam, 5-gate median filter (the quantities are filtered independently, even when used in a relationship such as the Z-ZDR rain rate estimate). KDP is derived from PhiDP after application of a 21-gate, along beam, iterative finite impulse response filter, with slope interval selection based upon reflectivity intensity (Hubbert and Bringi 1995).
Rain rates are in mm/hr. Literature references are provided at the end of this page. For an excellent review of radar estimated precipitation rates, see Brandes, 2000.
Note: rain rates will be re-processed following any final corrections to the radar calibration or Zdr bias.
The following summary of rain rate computations has been provided by Mike Dixon. In the equations:
Coefficients in the equations have been selected from previous studies of tropical rainfall.
Coefficients are from M. Katsumata and his MISMO analysis (private communication w/ C. Schumacher)
RATE_ZH = zh_aa * (ZH ** zh_bb)
where
zh_aa = 0.027366
zh_bb = 0.69444
For the reprocessed rain rate, it was found that the Brandes, et al. (2002) formulation produced more consistent results for the tropical Maldives environment than the in-field, real-time formulation. See Brandes, et al., eqn. 7. Note that the form of the equation used for the Z/Zdr relation is very sensitive to the value of the coefficients, particularly for low rain rates.
For the Z-ZH Rate used in the field, see the Footnotes.
ZDR is a linear ratio - (ZH / ZV).
RATE_Z_ZDR = zzdr_aa * (ZH ** zzdr_bb) * (ZDR ** zzdr_cc)
where
zzdr_aa = 0.00746
zzdr_bb = 0.945
zzdr_cc = -4.76
From Sachidananda and Zrnic, 1987 (eqn 9).
KDP in deg/km.
RATE_KDP = sign(KDP) * kdp_aa * (|KDP| ** kdp_bb).
where
kdp_aa = 40.6
kdp_bb = 0.866
Equation form from Ryzhkov and Zrnic, 1995, with coefficents determined by Brandes (personal communication w/ M. Dixon) for the tropical situation of CP2 radar and disdrometer data near Brisbane.
RATE_KDP_ZDR =
sign(KDP) * kdpzdr_aa * (|KDP| ** kdpzdr_bb) *
(ZDR ** kdpzdr_cc)
where
kdpzdr_aa = 136
kdpzdr_bb = 0.968
kdpzdr_cc = -2.86
The hybrid rate selects the "best" rain rate determination using logic similar to that set forth in Chandrasekar, et al (1990), Chadrasekar, et al. (1993), and extended by Ryzhkov, et al., 2005.
See Footnotes for the depricated, in-field hybrid rate calculation.
For the QC-version1, merged data set, the following logic was used to determine the hybrid precip rate:
_hybrid_aa = 10;
_hybrid_bb = 75;
_hybrid_cc = 100;
if (rateZh <= _hybrid_aa) {
rateHybrid = rateZh;
} else if (rateZZdr <= _hybrid_bb) {
rateHybrid = rateZZdr;
} else if (rateZZdr < _hybrid_cc) {
if (rateKdpZdr < 0.5 * rateZZdr) {
rateHybrid = rateZZdr;
} else if (rateKdpZdr > rateZZdr) {
rateHybrid = rateZZdr;
} else {
rateHybrid = rateKdpZdr;
}
} else {
if (rateKdp < 0.5 * rateZZdr) {
rateHybrid = rateZZdr;
} else {
rateHybrid = rateKdp;
}
}
Note: There is no clear support in the literature for the specific, chosen values of _hybrid_aa, bb or cc.
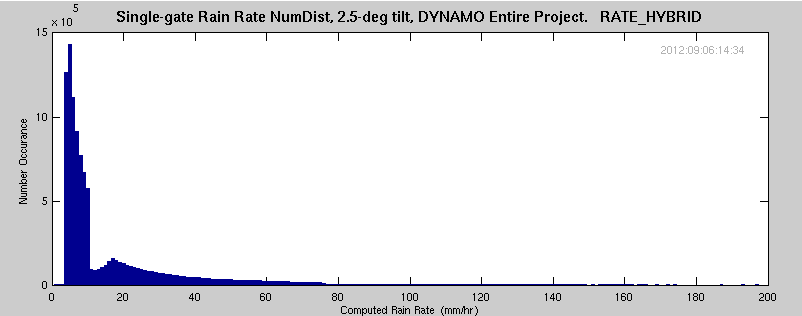
Note: There seem to be issues with the RATE_HYBRID, as calculated here. The precip rate distribution for the hybrid rate has a minimum near 10 mm/hr (for cases filtered on RATE_KDP exists). The problem seems to arise through the use of both RATE_ZH and RATE_Z_ZDR in making logical decisions: there are occasions where RATE_ZH > _hybrid_aa, but RATE_Z_ZDR is actually less than _hybrid_aa. This shifts some rates between about 10 < ZH < ~16 into a rate bin below 10 (for the specified _hybrid_aa = 10).
In the process of determining blockage of radar signal, the azimuthal precip accumulations were determined for the entire DYNAMO project. Additionally, the number distribution of the different rates was determined. These rates were selected for only those gates/occurances where there was valid data in the RATE_KDP field. This eliminates almost all occurances of light precip (RATE_KDP requires significant change in the differential phase, generally not measurable in light precip). The total number of data points is also reduced by this requirement.
Each of the following plots span data for almost all significant precip during the DYNAMO project. Data were filtered on RATE_KDP exists (light precip is eliminated). A total of approximately 10,300,00 data points are included for each plot.
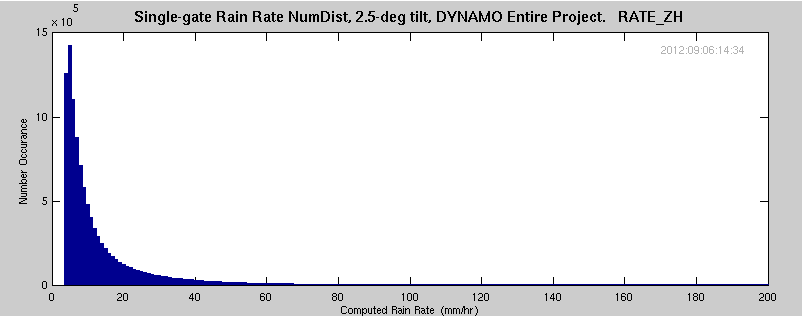
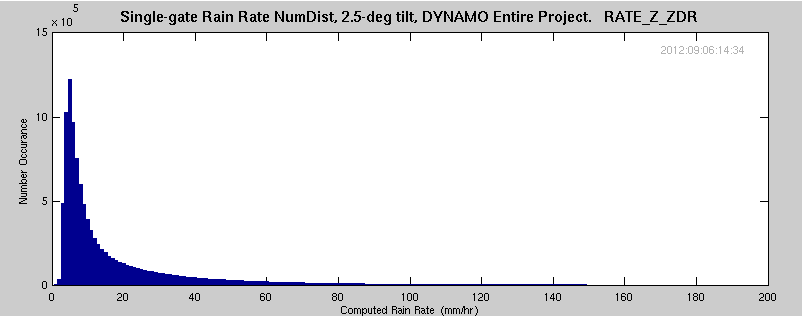
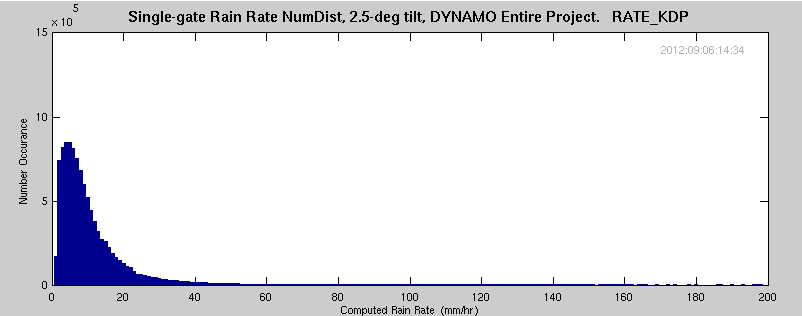
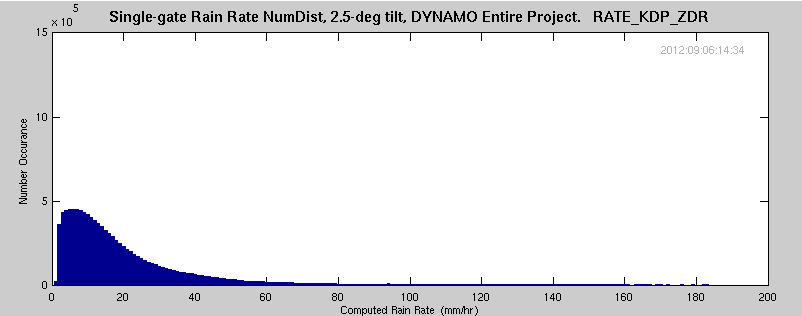
The following equation was used for the real-time precip estimate, but not for distribution with the final dataset. From Sachidananda and Zrnic, 1987:
ZDR is a linear ratio - (ZH / ZV).
RATE_Z_ZDR = zzdr_aa * (ZH ** zzdr_bb) * (ZDR ** zzdr_cc)
where
zzdr_aa = 0.00684
zzdr_bb = 1
zzdr_cc = -4.86
The following logic may have been used for the in-field hybrid precip rate determination. This logic was not used in determining the hybrid rate for the QC-version1 merged data set (see, above, for the conditions used for that data set).
RATE_HYBRID is computed following these rules:
If RATE_ZH <= hybrid_aa, RATE_HYBRID = RATE_ZH.
Else if RATE_Z_ZDR <= hybrid_bb, RATE_HYBRID = RATE_Z_ZDR.
Else If RATE_Z_ZDR <= hybrid_cc, RATE_HYBRID = RATE_KDP_ZDR.
Else if RATE_Z_ZDR > hybrid_bb, RATE_HYBRID = RATE_KDP.
where
hybrid_aa = 10
hybrid_bb = 50
hybrid_cc = 100
Note: It has been noticed that the hybrid rate seems to overestimate the rate when ZDR is lower than expected. For this data set we might need to consider changing the hybrid thresholds to not use RATE_KDP_ZDR and use RATE_KDP only for the higher rates.