Size Calibration of Single-Particle Light-Scattering Probes
(FSSP-100, FSSP-300, PCASP-100)
The operating principle of instruments that detect particles by the amount of light they scatter when passing through a focused light beam is based on the simple concept that the amount of light scattered by a particle is proportional to its size. The following discussion explains how the light gathered in the collecting optics of the instruments is subsequently converted to a size. Part of this discussion will explain where sources of uncertainty arise that limit the resolution of these types of instruments.
Briefly, this class of instruments, called optical particle counters (OPCs) from this point on, use a laser to illuminate a volume in the air stream. As the particles pass through the laser beam they scatter light. Some fraction of this is collected by the optics and focused on a photodiode. The peak amplitude of each pulse is compared with preset voltage thresholds, and a count is assigned to the bin number that corresponds to the channel numbers whose upper and lower thresholds bracket the pulse height value.
Since it is the scattered light we are measuring, we need a way to relate this to size. We need to assume the particle is spherical and to know the particle's refractive index, the intensity and wavelength of the illumination, the angles over which the light is collected, the efficiency of the detector and the electronic gain. With this information we can use Mie scattering theory to calculate the relationship between the pulse height measured and particle size. Since we don't precisely know the illumination and detector efficiency, an empirical calibration is required to assign sizes to each of the pulse-height thresholds that have been set in the instruments.
If we have calibration particles whose size we can strictly control, then we can sample these particles with the probe and get a relationship between particle size and voltage threshold. The ideal method would be the possibility of generating particles with the refractive index of atmospheric particles we plan to measure. We could start with the lowest size threshold and adust the size until we only detect particles in the first channel. This would then define the size threshold of the first channel. Subsequent adjustments would then calibrate the higher bin sizes. Unfortunately, for instruments that measure water, like the FSSP-100, generating such a precise size of droplet is very difficult (but not impossible). For most routine calibration most researchers have substituted less-volatile particles for water and then made adjustments for the difference in refractive index. For example, commercially-available glass beads, with well-controlled sizes, are the normal calibration particle used. In principle, we should be able to select a range of glass bead sizes, convert them to their water equivalent size (Glass and water scatter light differently, so we have to know what size water particle will scatter the same amount of light as a particular glass bead size) and perform the threshold calibration as described above.
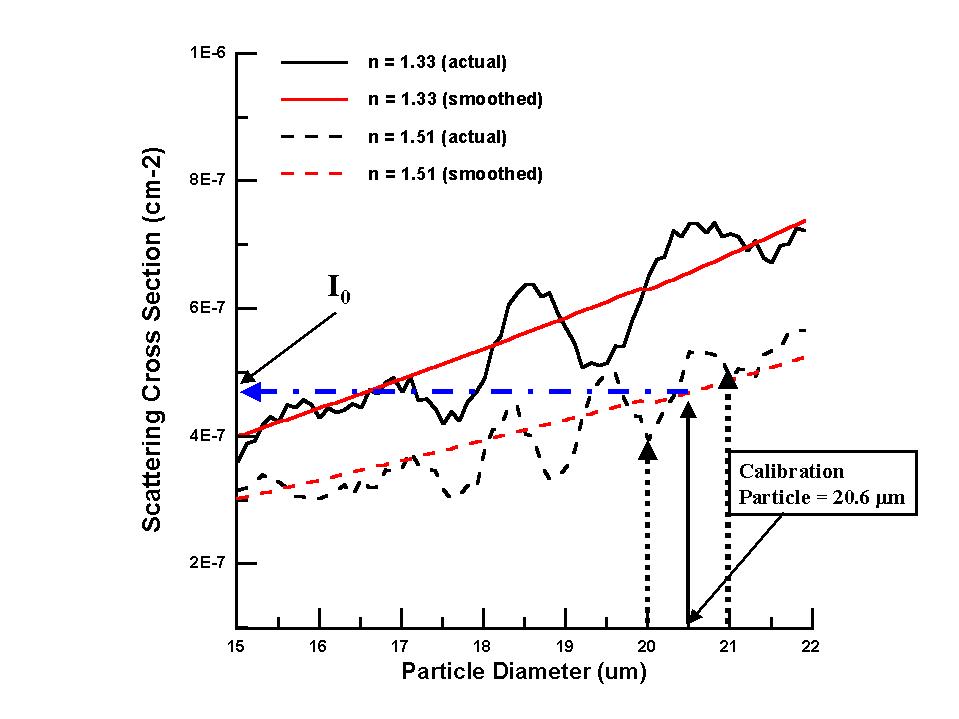
Two issues complicate this concept. One, the amount of scattered light is dependent on the index of refraction of the droplet or particle as well as its size. Two, in certain size ranges the scattered light does not increase monotonically with size. Figure 1 illustrates these two points.

In this figure we see that glass particles (refractive index, n=1.51), in the size range shown, scatter less light than water droplets (n = 1.33). Secondly, it can be seen that, at some sizes, particles scatter less light than smaller particles. This complication leads to a big problem when trying to use glass beads as a surrogate for water. In the Fig. 1 example, a commercially-available glass bead with a size of 20.6 µM, has a scattering cross section of approximately 5x10-7 cm-2. We can see that several sizes of water droplets scatter the same amount of light, i.e. 16.5, 17, and 18 µM water droplet scatter approximately the same amount of light (intersection points of horizontal blue line). In addition, the size of the calibration beads are only controlled to approximately ñ1%, and inhomogeneities in the intensity of the laser beam add to the uncertainty in measured light, so a conversion to water equivalency could produce a range of possible water droplet sizes from approximately 15 - 19 µM. This is too much uncertainty to determine the voltage thresholds of the instruments. Therefore, we take a different approach that sidesteps this problem.
If we believe the Mie scattering theory, and I think we do, since it has been verified experimentally in many laboratory studies, we can convert the voltage thresholds of the OPCs with only a single-point measurement. The procedure is as follows:
Again, in principle, this appears quite straight forward, but the multivalued nature of the scattering cross section of particles complicates things. What size do you assign to a voltage threshold when several sizes can produce the same amount of scattered light (Fig. 2)?
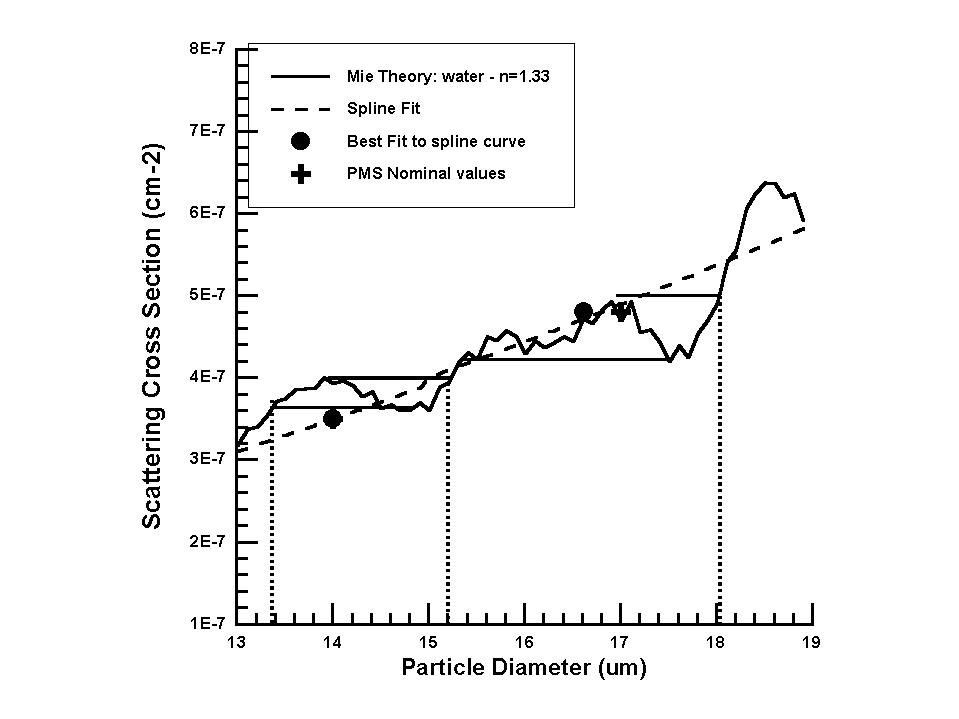
One possibility is to adjust the voltage thresholds so they bracket the multivalued region. For example, as shown in Figure 2., the vertical dashed lines are selecting regions that insure that particles won't be incorrectly placed in lower-size bins. This technique is preferable, but the problem we must face at the time being, and when using OPC data from previous measurement campaigns, is that a different technique was used by the manufacturer of these probes. Instead of adjusting voltage thresholds to bracket the multivalued regions, the theoretical scattering cross sections were smoothed to produce a monotonically-increasing function, and then the voltage thresholds were set to values where the channels would correspond to evenly-spaced sizes. Figure 3 shows several size bins of the FSSP-100 as set up by PMS in range 0.
This method of setting the channels provides nice-size intervals but masks the fact that there is a fair degree of uncertainty associated with these size intervals, e.g., a certain fraction of particles in size range 11 - 14 µM will actually get sized in the 14-17 µM size range, while there will be some particles in the 14-17 µM size range that end up in the lower channel. This lends uncertainty in the sizing of particles by the FSSP and subsequent calculation of the LWC that depends on the 3rd power of the diameter. Since we can calculate these fractions of under- and over-sizing in the instrument, it should be possible to do inversions on the spectra and obtain a better estimate of thee sizes. No one has actually attempted this yet, as far as I am aware.
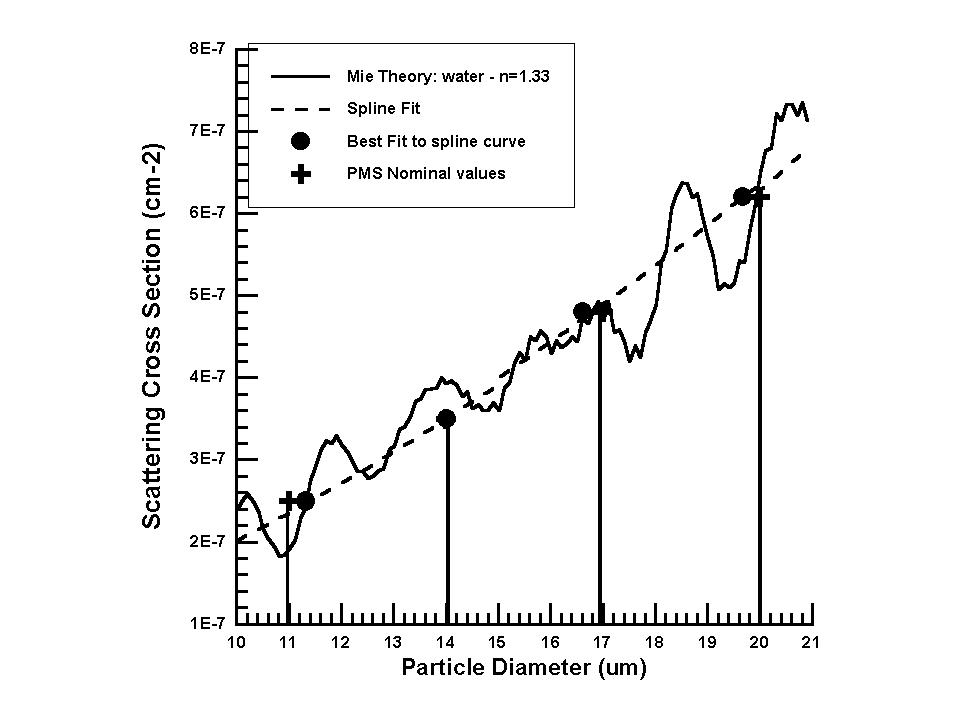
The final point to make about this calibration methodology is that, in developing it and running the most up-to-date Mie scattering code that I could find, I discovered that size channels that are specified by PMS are in error at sizes larger than 30 µM. As shown in Fig. 4, when the voltage threshold that are preset in the FSSP are converted to scattering cross section values and related to droplet size at the refractive index of water, the sizes predicted by scattering theory diverge from those specified by PMS at sizes > 30 µM.
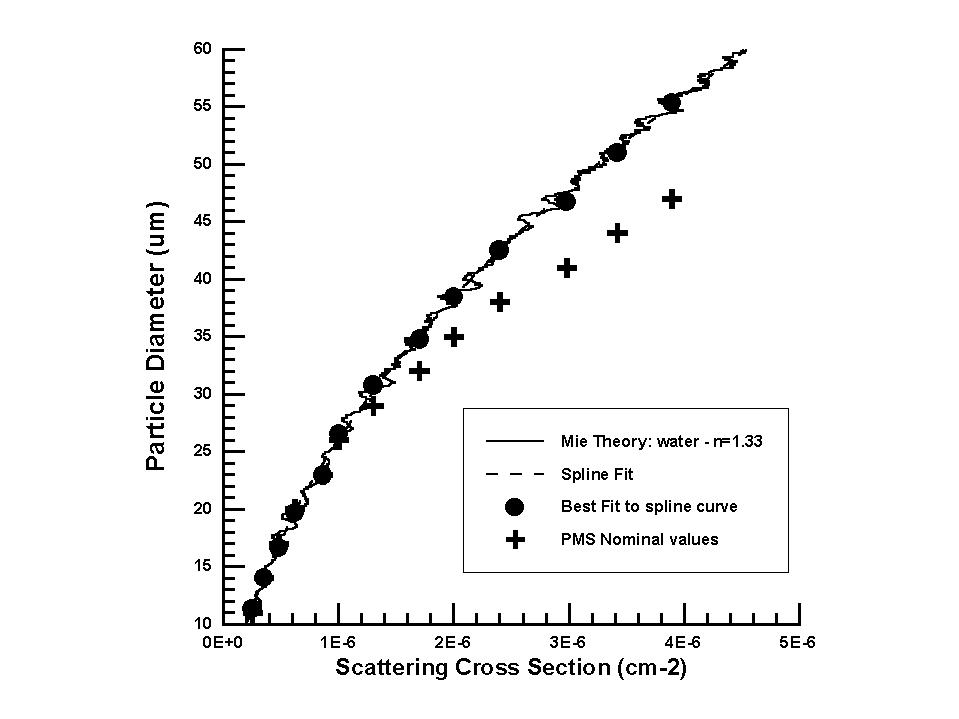
Jim Dye made measurements years ago with a single-droplet generator and had noticed the same thing (Dye and Baumgardner, 1984), i.e., that the FSSP was undersizing the larger droplets. Thus, this is why the size thresholds that I provide for the FSSPs are always larger at the upper end. I am currently preparing a small note to JTECH on this subject.
The software that I provided you "setFSSP100channels" to set the size thresholds, is a C program that automatically performs the steps outlined above. All you need is the calibration information from the technicians and you will be able to set up the FSSP-100 for any project. I have similar codes for the PCASP and FSSP-300 that I will give you, as well.
Dye, J.E. and D. Baumgardner, 1984: Evaluation of the forward scattering spectrometer probe: I. Electronic and optical studies. J. Atmos. Ocean. Tech., 1, 329-344.