









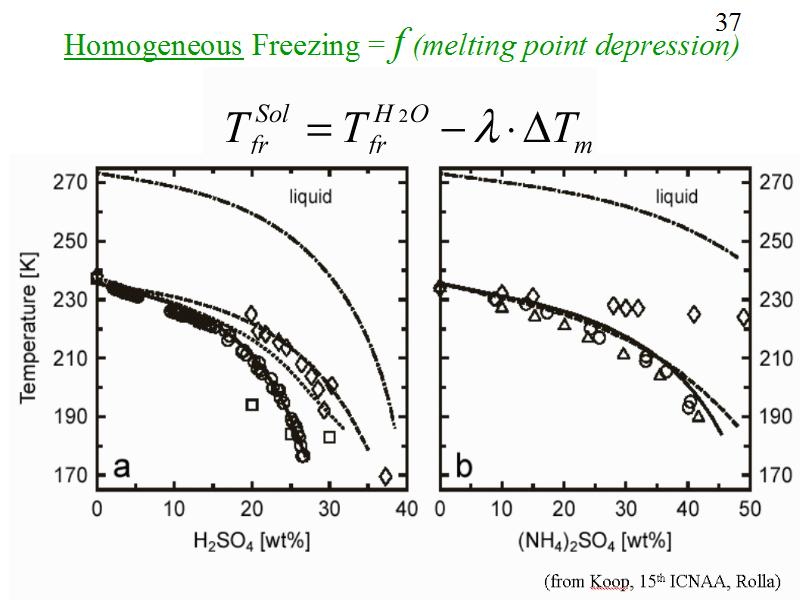
A simple empirical relationship has been found for the homogeneous freezing of aqueous solutions such as sulfuric acid or ammonium sulfate. Lambda is an empirical constant equal to about 1.7.
This figure is also from Koop.
FIGURE 2. Comparison of ice nucleation measurements and models for micron sized aqueous droplets
of (a) H2SO4 and (b) (NH4)2SO4. Diamonds: FTIR experiments;16,17 circles: microscope
experiments;18,19 triangles: emulsion experiments;19-21 squares: electrodynamic balance experiments.22
Dash-dotted line: equilibrium ice melting point curve; dotted line: classical nucleation model for
H2SO4-H2O;23 dashed line: lambda model, see text;25-27 solid line: thermodynamic model, see text.28
The dashed curves indicate results from a model 25-27 in which the freezing
temperature of a solution droplet, Sol
fr T , was calculated according to
, m
2O H
fr
Sol
fr T T T (1)
where H
fr T
2O
is the freezing temperature of a pure water droplet of the same size, m T
is the equilibrium melting point depression of ice in the solution (i.e., Sol
m 273.15-T ),
and is a constant depending on the nature of the solute. The homogenous ice
nucleation rate coefficient in solution, Sol
fr J , is predicted based on the assumption that
), ) 2O H
fr
2O H
fr
Sol
fr
Sol
fr (T J (T J (2)
where ) 2O H
fr
2O H
fr (T J is the homogeneous ice nucleation rate coefficient for pure water,
H
fr J
2O
, at temperature H
fr T
2O
. In the following paragraphs this model will be termed the
“lambda model”. The curves in Figure 2 represent a homogeneous nucleation rate of
J=10 9 cm -3 s -1 and a value of =1.0 for the H2SO4 case, and =1.7 for the (NH4)2SO4
case.27 The formulation of Pruppacher 6 for (T) f J 2O H
fr has been used in these
calculations.
The solid curves indicate the results of a semi-empirical thermodynamic ice
nucleation model which is based on experimental ice freezing data of 18 different
solutes in aqueous solutions.28 This model will be termed the “thermodynamic model”